لطالما نظرنا إلى الرياضيات على أنها لغة الكون الصارمة، الحصن المنيع لليقين حيث 1+1 يساوي دائماً 2، وحيث لا مجال للعواطف أو التأويلات الشخصية. إنها العالم الذي نلجأ إليه عندما نحتاج إلى إجابات قطعية لا تقبل الشك. ولكن، ماذا لو قلنا لك أن خلف هذا الستار من المعادلات الموزونة والنتائج الدقيقة، يختبئ عالم آخر؟ عالم غريب ومثير، مليء بالثغرات المنطقية والنتائج التي تبدو للوهلة الأولى “مستحيلة” تماماً، رغم أنها صحيحة رياضياً. مرحباً بكم في عالم “المفارقات الرياضية” (Mathematical Paradoxes).
المفارقة في جوهرها ليست خطأً حسابياً، بل هي استنتاج يبدو متناقضاً مع نفسه أو مخالفاً للمنطق السليم وبديهتنا اليومية، على الرغم من أنه يستند إلى مقدمات تبدو صحيحة تماماً وقواعد منطقية سليمة. إنها اللحظة التي يقول فيها عقلك “هذا لا يمكن أن يكون صحيحاً”، بينما تصرخ المعادلات قائلة “بل هو كذلك!”.
المحتويات
ما هي المفارقات الرياضية ولماذا تهمنا؟

تمثل المفارقات الرياضية مواقف منطقية تبدو فيها النتيجة متناقضة أو مستحيلة رغم صحة المقدمات. تختلف هذه الظواهر عن الأخطاء البسيطة؛ إذ تكشف عن ثغرات عميقة في فهمنا للمنطق الرياضي والواقع.
لا تقتصر أهمية هذه المعضلات على كونها ألغاز رياضية مسلية فحسب، بل ساهمت في تطوير فروع كاملة من الرياضيات الحديثة. دفعت العلماء لإعادة النظر في المفاهيم الأساسية، وأدت لاكتشافات غيرت مسار العلم.
لماذا تحدث المفارقات؟
تنشأ المفارقات عادة من:
- افتراضات خاطئة نعتبرها بديهية دون تمحيص
- قصور في لغتنا المنطقية أو الرياضية
- محاولة تطبيق قواعد محدودة على حالات لا نهائية
- الخلط بين المستويات المنطقية المختلفة
مفارقة زينون: عندما يتوقف الزمن والحركة

يعود الفيلسوف اليوناني زينون الإيلي (القرن الخامس قبل الميلاد) بواحدة من أقدم وأشهر المفارقات. تحدى زينون فكرة الحركة ذاتها من خلال سلسلة من الحجج الذكية.
مفارقة أخيل والسلحفاة
تصور أن أخيل، أسرع عداء في الأساطير اليونانية، يتسابق مع سلحفاة بطيئة. منح السلحفاة فرصة البدء قبله بمسافة 100 متر. يقول زينون: عندما يصل أخيل للنقطة التي بدأت منها السلحفاة، تكون قد تقدمت مسافة صغيرة. وعندما يصل لتلك النقطة الجديدة، تتقدم مرة أخرى. تستمر هذه العملية إلى ما لا نهاية!
يبدو الاستنتاج مجنوناً: لن يتمكن أخيل أبداً من اللحاق بالسلحفاة، رغم أننا نعرف من الواقع أنه سيتجاوزها بسهولة.
الحل الحديث
انتظر العالم أكثر من ألفي عام للحصول على تفسير مقنع. جاء الحل مع تطور حساب التفاضل والتكامل في القرن السابع عشر. أثبت علماء الرياضيات أن مجموع سلسلة لانهائية من الأرقام يمكن أن ينتج رقماً محدوداً.
على سبيل المثال: 1/2 + 1/4 + 1/8 + 1/16 + … = 1
بهذا المفهوم، يقطع أخيل مسافة محدودة في زمن محدود، حتى لو قسمناها لأجزاء لا نهائية. كشفت مفارقة زينون عن حاجتنا لفهم أعمق لمفهوم اللانهاية، مما ساهم في تطور فلسفة الرياضيات بشكل جذري.
معضلة مونتي هول: عندما يخالف الاحتمال الحدس
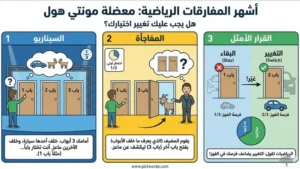
تنتقل بنا الرحلة للقرن العشرين، حيث ظهرت واحدة من أكثر المفارقات إثارة للجدل في تاريخ الرياضيات الحديثة. استمدت معضلة مونتي هول اسمها من برنامج تلفزيوني أمريكي شهير.
كيف تعمل اللعبة؟
تخيل أنك في برنامج مسابقات، وأمامك ثلاثة أبواب مغلقة:
- خلف أحد الأبواب سيارة فاخرة
- خلف الآخرين ماعز
تختار باباً، لنقل الباب رقم 1. يعرف مقدم البرنامج ما خلف كل باب، فيفتح باباً آخر (مثلاً الباب رقم 3) ليظهر ماعزاً. ثم يسألك: هل تريد تغيير اختيارك للباب رقم 2؟
الإجابة المفاجئة
يظن معظم الناس أن احتمالية الفوز متساوية سواء غيرت اختيارك أم لا (50-50). لكن الحقيقة الرياضية مختلفة تماماً:
- إذا حافظت على اختيارك الأول: احتمالية الفوز = 1/3
- إذا غيرت اختيارك: احتمالية الفوز = 2/3
تضاعف فرصك بالفوز عند تغيير الاختيار! حتى بعض علماء الرياضيات رفضوا هذه النتيجة في البداية.
لماذا يصعب قبول الحل؟
يكمن السر في أن مقدم البرنامج لا يفتح باباً عشوائياً، بل يفتح دائماً باباً يحتوي على ماعز. هذه المعلومة الإضافية تغير الاحتمالات بشكل جذري. عندما اخترت في البداية، كانت احتمالية أن تكون السيارة خلف أحد البابين الآخرين هي 2/3. بعد فتح أحدهما، تنتقل كل هذه الاحتمالية للباب المتبقي.
مفارقة الحلاق: تحطيم أسس المنطق

قدم الفيلسوف والرياضي البريطاني برتراند راسل هذه المفارقة عام 1901، محدثاً زلزالاً في أسس المنطق الرياضي.
تقول المفارقة: في قرية صغيرة، يوجد حلاق واحد يحلق لحى جميع الرجال الذين لا يحلقون لحاهم بأنفسهم، فقط هؤلاء. السؤال: من يحلق للحلاق؟
- إذا حلق لنفسه، فهو ضمن من يحلقون لأنفسهم، وبالتالي يجب ألا يحلق لنفسه
- إذا لم يحلق لنفسه، فهو ضمن من لا يحلقون لأنفسهم، وبالتالي يجب أن يحلق لنفسه
التأثير على الرياضيات
أظهرت مفارقة راسل ومشتقاتها وجود مشكلات خطيرة في نظرية المجموعات الساذجة. أدى ذلك لتطوير نظريات رياضية أكثر صرامة، وإلى إعادة بناء أسس الرياضيات على قواعد منطقية أكثر دقة.
مفارقة الفندق اللانهائي لهيلبرت
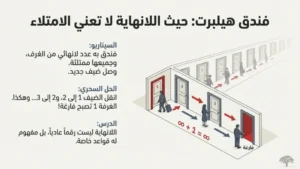
ابتكر عالم الرياضيات الألماني ديفيد هيلبرت هذه المفارقة الساحرة لتوضيح طبيعة اللانهاية.
تخيل فندقاً يحتوي على عدد لانهائي من الغرف، جميعها مشغولة. يصل ضيف جديد ويطلب غرفة. هل يمكن إيواؤه؟
الحل المدهش: نعم! يطلب المدير من الضيف في الغرفة 1 الانتقال للغرفة 2، والضيف في الغرفة 2 ينتقل للغرفة 3، وهكذا. تصبح الغرفة 1 خالية للضيف الجديد.
بل والأكثر دهشة: يمكن استيعاب عدد لانهائي من الضيوف الجدد! ببساطة، ينتقل كل ضيف للغرفة ذات الرقم المضاعف (من الغرفة n إلى الغرفة 2n)، فتصبح جميع الغرف الفردية خالية.
توضح هذه المفارقة أن اللانهاية لا تتصرف كالأعداد العادية، وأن حجم مجموعة لانهائية لا يتغير بإضافة عناصر جديدة.
مفارقة عيد الميلاد: الاحتمالات تخدع البديهة
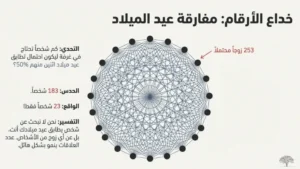
تسأل هذه المفارقة: كم شخصاً تحتاج في غرفة واحدة حتى يكون احتمال أن يتشارك اثنان منهم نفس عيد الميلاد أكثر من 50%؟
معظم الناس يظنون أنك تحتاج لحوالي 183 شخصاً (نصف أيام السنة تقريباً). لكن الإجابة الصحيحة مفاجئة: فقط 23 شخصاً!
مع 23 شخصاً، يصل الاحتمال لحوالي 50.7%. ومع 70 شخصاً، يصل لأكثر من 99.9%.
يكمن السبب في أننا لا نبحث عن شخص محدد يتشارك عيد ميلادك، بل عن أي زوج من الأشخاص يتشاركان عيد الميلاد. عدد الأزواج المحتملة يزداد بسرعة: مع 23 شخصاً، هناك 253 زوجاً محتملاً.
كيف تساعدنا المفارقات على التفكير بشكل أفضل؟

تقدم لنا المفارقات الرياضية دروساً قيمة تتجاوز عالم الأرقام:
تطوير التفكير النقدي
تعلمنا ألا نثق عمياً في حدسنا الأول. ما يبدو بديهياً قد يكون خاطئاً، وما يبدو مستحيلاً قد يكون حقيقة رياضية.
فهم حدود المنطق
تكشف المفارقات عن الحاجة للدقة في صياغة المفاهيم والقواعد. كلمة واحدة أو افتراض صغير قد يغير كل شيء.
التواضع المعرفي
حتى أعظم العقول وقعت في فخ المفارقات. تذكرنا بأن المعرفة رحلة مستمرة، وأن الأسئلة أحياناً أهم من الإجابات.
المفارقات في العصر الحديث
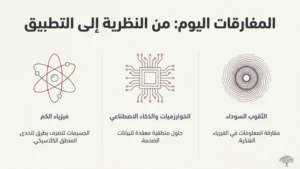
لا تزال المفارقات الرياضية تحفز البحث العلمي حتى اليوم. تظهر في:
- نظرية الكم، حيث تتصرف الجسيمات بطرق تتحدى المنطق الكلاسيكي
- علوم الحاسوب، خاصة في دراسة الخوارزميات والذكاء الاصطناعي
- النظرية الاقتصادية، مثل مفارقة سانت بطرسبرغ في نظرية القرار
- الفيزياء النظرية، كمفارقة المعلومات في الثقوب السوداء
نصائح لفهم المفارقات الرياضية
إذا أردت التعمق في هذا العالم الساحر:
ابدأ بالأمثلة البسيطة وحاول حلها بنفسك قبل البحث عن الإجابة. تساعد المحاولة الشخصية على فهم أعمق.
استخدم الرسوم البيانية والنماذج المادية عندما أمكن. تجسيد المفارقة يجعلها أسهل للاستيعاب.
ناقش المفارقات مع الآخرين. غالباً ما تظهر زوايا جديدة للمشكلة من خلال الحوار.
لا تستسلم بسرعة. بعض المفارقات استغرقت قروناً لحلها، فلا بأس ببعض الوقت للتأمل.
خاتمة: جمال الحيرة الرياضية
تمنحنا المفارقات الرياضية فرصة نادرة لاستكشاف حدود فهمنا وتوسيعها. ليست مجرد ألغاز رياضية للتسلية، بل نوافذ تطل على طبيعة المنطق والواقع نفسه.
كلما تعمقنا في هذه المعضلات، أدركنا أن الرياضيات ليست مجموعة جامدة من القواعد، بل محيط حي يتطور باستمرار. كل مفارقة تُحل تفتح أبواباً جديدة من الأسئلة، وكل سؤال يقودنا لفهم أعمق لهذا الكون المدهش.
في النهاية، تذكرنا المفارقات بأن العلم والمعرفة رحلة لا تنتهي، وأن أجمل لحظات الاكتشاف تأتي عندما نواجه شيئاً يهز قناعاتنا ويدفعنا للتساؤل: ماذا لو كان كل ما نعرفه مجرد بداية؟

